Skip to the graphs, the full results and methodology, or read on to discover how Lurk has evolved to empower developers with unparalleled performance and usability in zero-knowledge programming.

Just over three years ago, we set out to create Lurk with the goal of making it the best zk programming language — a tool that would make it easier for developers to leverage the power of zero-knowledge proofs in their applications.

To us, being the best meant excelling in several key areas:

• Expressive Turing-completeness, enabling users to write versatile and powerful programs.
• Ease of authoring and auditing proof programs, making development and maintenance more straightforward.
• Support for standard, persistent, private data, giving users secure and consistent control over their data.
• Performance — a suite of interrelated properties designed to minimize latency, memory consumption, capital expenditure (CaPex), and operational expenses (OpEx), while maximizing throughput and scalability.

The first version of Lurk laid a strong foundation in terms of expressiveness, ease of use, and data privacy. However, we knew that performance was an area where we would face intense competition from other zkVM projects.

Our approach to performance has been multi-faceted:

• The Lurk language is designed to express semantics minimally, directly translating into concise and efficient proofs. By focusing on proving exactly what the programmer intends, we minimize costs and improve performance.
• We embraced folding schemes through Nova, which promised excellent performance in zkVMs like Lurk.
• We aimed to integrate NIVC (Non-Interactive Verifiable Computation) to allow for high-performance cryptographic computations to be scripted by Lurk—a critical component for achieving best-in-class performance.

Our bet on Nova, though it was a very new technology at the time, was driven by our vision to bring the highest-performing zkVM to our users. This led us to develop Arecibo, our first observatory prover backend, which played a key role in polishing an early version of SuperNova and bringing NIVC online. Alongside ongoing optimization efforts, these initiatives allowed us to make good progress with our Lurk Beta release.

However, benchmarks remained a crucial but elusive measure of our progress. The Fibonacci benchmark, though not entirely representative of Lurk’s real-world usage, emerged as an industry-standard for measuring zkVM performance. While it posed challenges, it also fueled our creativity and led us to develop new solutions.

In December 2023, we introduced Memoset, our abstraction for integrating lookup arguments into Lurk. This innovation addresses circuit-packing challenges, reduces the cost of hashing in Lurk’s data model, and unlocks memoization —- a powerful optimization for functional algorithms.

---

Then, in late February 2024, Succinct Labs made a splash with their SP1 blog post claiming that their alpha release was ‘up to 28x faster for certain programs’. After running some benchmarks locally, it became clear that we were 55x slower than SP1 on the Fibonacci test. This performance gap was a disservice to our hypothetical users, and it prompted a pivotal shift in our approach.

In response, we focused our efforts on addressing these performance issues head-on. In late March, we decided to attack the immediate performance needs for our light clients with Sphinx, our second observatory backend, while simultaneously porting our Memoset and core Lurk development to use the same backend. This one-two punch of STARKs and Memoset became crucial in transforming Lurk into the high-performance zkVM we envisioned.

Now, after almost six months of intensive work, we’re proud to release Lurk 0.5. This release marks a significant step forward, with a language and zkVM that fully exploit program structure to avoid redundant computation through functional memoization. While there are still important optimizations ahead, we are excited to demonstrate Lurk’s excellence across all the necessary categories for a leading zk programming language.

As you explore the benchmarks below, keep in mind that every improvement and optimization we’ve made is aimed at making the Lurk user-experience more powerful, efficient, and effective.

---

The Graphs

Our benchmark selection here is mostly geared toward illustrating problems for which Lurk’s adaptations make it well-suited. The most interesting comparisons are between Lurk and Sphinx. Because they share the same backend codebase, these comparisons provide the best apples-to-apples comparison between Lurk and RISC-V performance. We ran all benchmarks with default parameters, as well as two alternate configurations to tease out observable differences.

Also potentially interesting are the differences between Sphinx and SP1 — although intended to be transient (we aspire to be good open-source citizens, to SP1 as to Nova before it). These reflect Argument’s ethos of engineering and innovation.

Finally, we’ve included Risc0 and Jolt in order to provide a picture of how other RISC-V backends perform. Where these implementations excel, it may be instructive to consider the result of porting Lurk to them. Remember, Lurk is a language first and foremost — promoting correctness and performance by design. Argument is committed to performance and to ensuring Lurk can always run on competitive contemporary provers, just as our recent work demonstrates.

NOTE: in all benchmarks below, lower is better.

fib

The dreaded Fibonacci. Lurk isn’t quite the fastest, but Sphinx is.

As a point of interest, check the Lurk source. We implement the most naive recursive algorithm but perform in the same class as the imperative, looping implementation you expect to perform well.

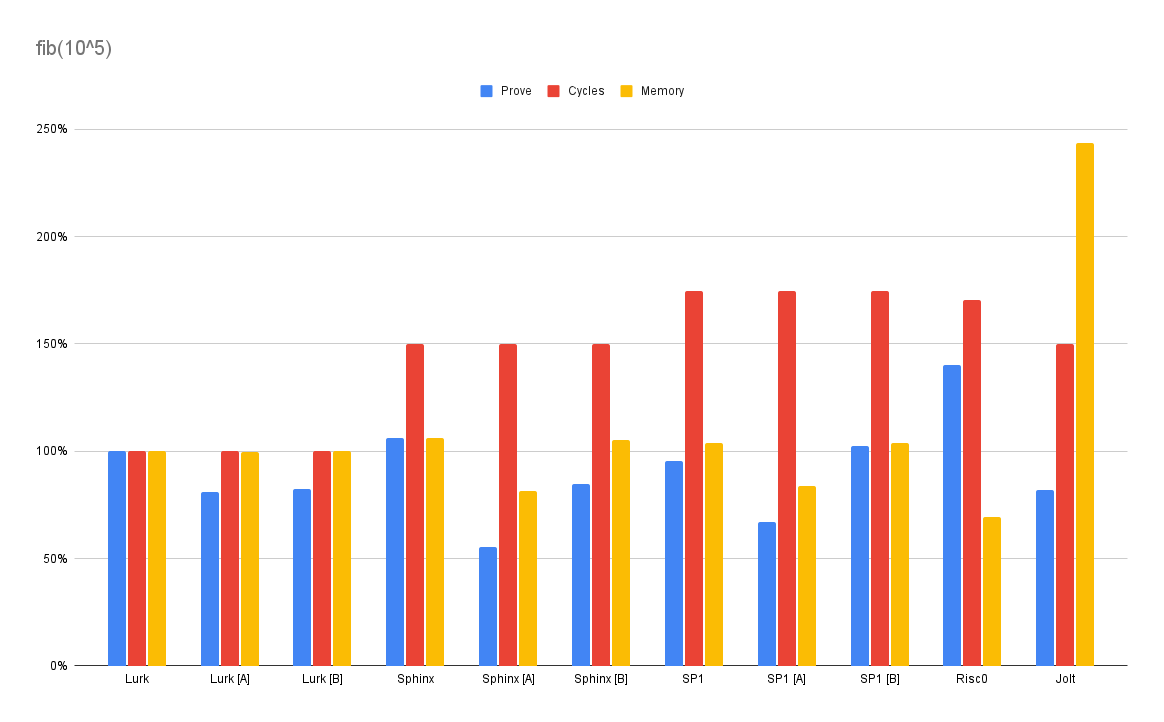source: Lurk (5 LOC), Rust (8 LOC)

---

lcs

Longest common subsequence (lcs) is an important real-world algorithm, underlying, for example, the diff program. It is also an example of dynamic programming — a technique which can especially benefit from Lurk’s memoization. Note that RISC-V cannot natively memoize because of its dependence on mutable memory.

The Lurk program is only 12 lines, most of which is a simple transcription of the algorithm’s description.

By contrast, the Rust program must either explicitly memoize at the program level — or, more efficiently, build an explicit table.

Note that even though the Rust program uses the more efficient (for an imperative language) tabling strategy, Lurk outperforms the RISC-V implementations.

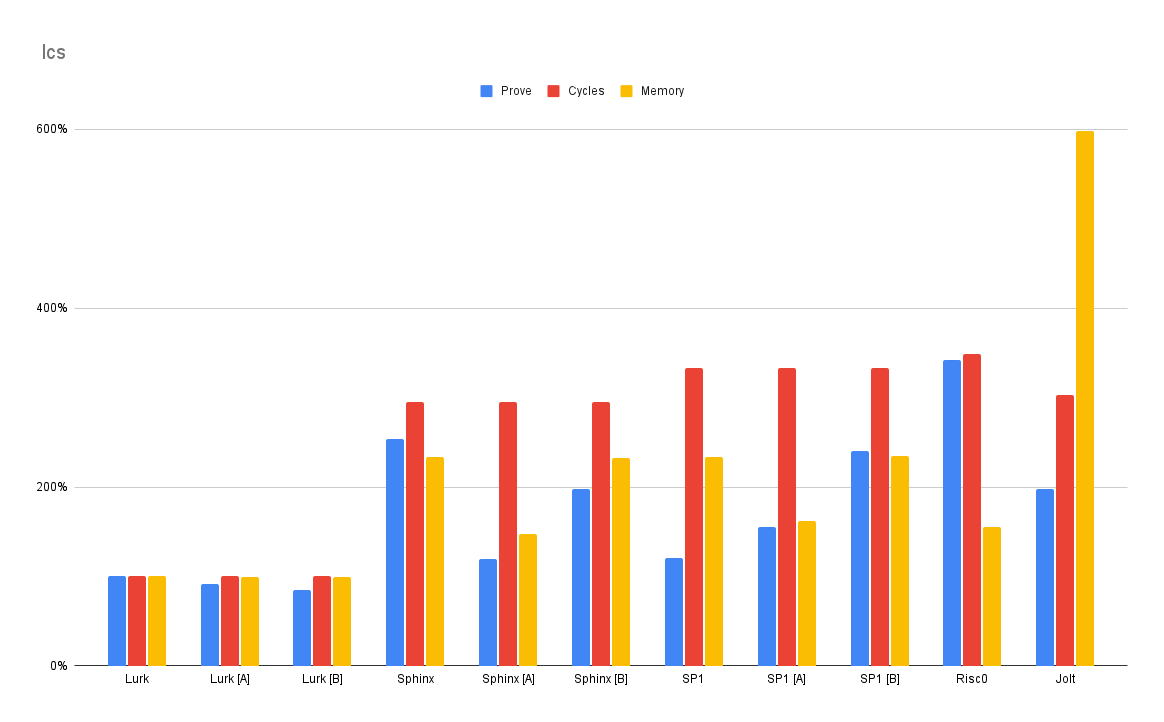source: Lurk (12 LOC), Rust (42 LOC)

---

lcs2

Because the effect of compilation can be opaque, it’s hard (especially when working with a relatively novel target like RISC-V) to know how an implementation will perform. Here we tried an alternate, somewhat simpler Rust program — but it performed worse.

Interestingly, the simpler Lurk program frequently tends to be the better-performing one. To a first approximation, Lurk lets you ‘say what you mean’, and performance comes for free with the intent-based reduction strategy.

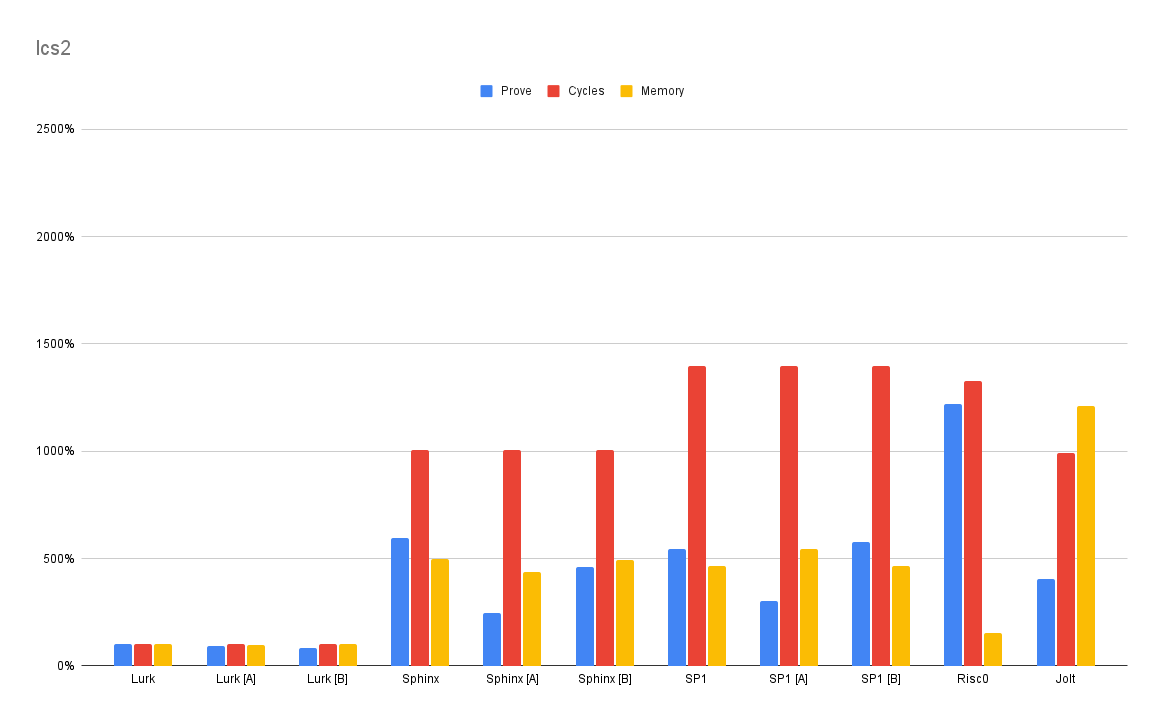source: Rust (33 LOC)

---

sum

Although this benchmark is called sum, it mainly exercises a VM’s ability to handle large input. Lurk was designed from the ground up to natively process content-addressed data (Merkle DAGs), so it’s no surprise that it’s 5x faster than Sphinx and 10x faster than the next nearest competitor (Jolt).

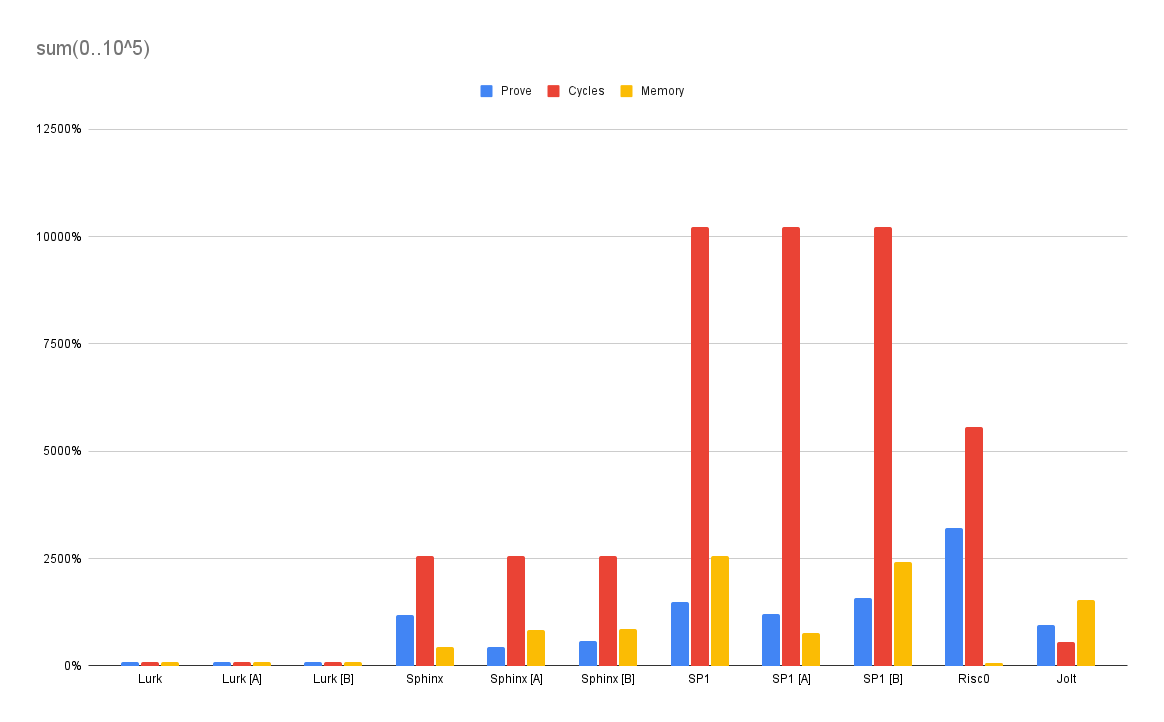source: Lurk (3 LOC) Rust (1 LOC)

---

fastfib

Life is more than just cycle counts and frequencies. Wouldn’t it be nice to just calculate Fibonacci fast? This benchmark will compute Fibonacci for the largest u64 with a prescribed (but speedy) algorithm — efficiently exponentiating a rank 2 square matrix. Unlike the dynamic programming problems, this one is lean and clear in Rust:

// [0, 1, 2, 3] = |0 1|
//                |2 3|
type Matrix2x2 = [u64; 4];

fn matmul(a: Matrix2x2, b: Matrix2x2) -> Matrix2x2 {
    [
        a[0] * b[0] + a[1] * b[2],
        a[0] * b[1] + a[1] * b[3],
        a[1] * b[0] + a[3] * b[2],
        a[2] * b[1] + a[3] * b[3],
    ]
}

fn fast_matexp(mut b: Matrix2x2, mut e: u64) -> Matrix2x2 {
    let mut acc = [1, 0, 0, 1]; // identity matrix

    while e > 0 {
        if e % 2 == 1 {
            // odd?
            acc = matmul(b, acc);
            e = (e - 1) / 2;
        } else {
            e = e / 2;
        }
        b = matmul(b, b);
    }
    acc
}

fn fib(n: u64) -> u64 {
    fast_matexp([0, 1, 1, 1], n + 1)[0]
}

And the Lurk is almost directly equivalent this time, in accordance with this Fibonacci specification.

(letrec ((matmul (lambda (a b) ;; 2x2 matrix multiplication
                   (cons (cons (+ (* (car (car a)) (car (car b)))
                                  (* (cdr (car a)) (car (cdr b))))
                               (+ (* (car (car a)) (cdr (car b)))
                                  (* (cdr (car a)) (cdr (cdr b)))))
                         (cons (+ (* (car (cdr a)) (car (car b)))
                                  (* (cdr (cdr a)) (car (cdr b))))
                               (+ (* (car (cdr a)) (cdr (car b)))
                                  (* (cdr (cdr a)) (cdr (cdr b))))))))
         (fast-matexp (lambda (b e)
                        (if (= e 0)
                            '((1 . 0) . (0 . 1)) ;; identity matrix
                            (if (= (% e 2) 1) ;; (odd? e)
                                (matmul b (fast-matexp (matmul b b) (/ (- e 1) 2)))
                                (fast-matexp (matmul b b) (/ e 2))))))
         (fib (lambda (n)
                (car (car (fast-matexp '((0 . 1) . (1 . 1)) (+ n 1)))))))
  (fib 18446744073709551614))

Was mich nicht umbringt, macht mich stärker. Thank you, Fibonacci, for challenging us to do our best. Lurk takes this hands down — a bit over a quintillion times faster (from fib(~10^1) to fib(~10^19)) than when we started. And with just a little bit of cheating. But what’s a better algorithm between friends?

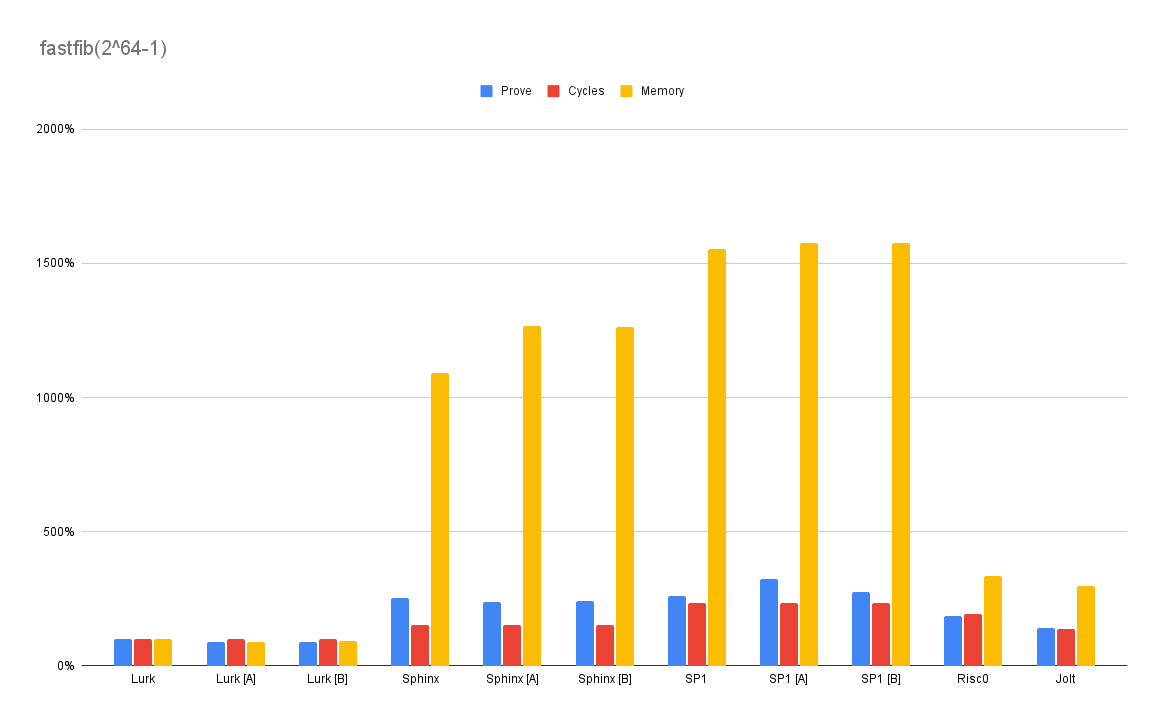source: Lurk (18 LOC), Rust (32 LOC)

---

Conclusion: Look Ma, no Compiler

As a parting thought, please remember that all Lurk benchmarks above are purely interpreted. Lurk avoids the significant risks, costs, and complexities associated with ahead-of-time compilation for zero-knowledge proofs. This simplistic choice shows in our source code which (if you can read Lisp) clearly demonstrates that it’s not necessary to bend over backwards to please the borrow checker, or to coerce the compiler into producing performant code.

We’ve shown you don’t need compilation, but that doesn’t mean compilation cannot be an incredibly valuable tool — both for correctness and for performance. Compilation needs to be put into context and folded into the stack in a way that adds value in all categories we require of our zk programming language. We just don’t happen to believe RISC-V is the right target to highlight that value. In the fullness of time, we hope to show you what we mean.

---

Full Results and Methodology

Table of Contents

• Overview
• Benchmark Results
  • Fibonacci
    • Regular fibonacci
    • Fast fibonacci
  • Sum
  • LCS
    • lcs
    • lcs2
• Config
  • Environment Variables
    • Default
    • A
    • B
  • Security Level
  • Specs
• Notes

Overview

This report shows the CPU-only (no GPU acceleration) benchmarks for Lurk 0.5, Sphinx, SP1, Risc0 and Jolt. These results were obtained with commit 97d8ac620fc9c90139dce6aa45c8856f444d2d2d.

Benchmark Results

Times are in seconds, memory is in GiB. Lurk cycles are approximated by the number of calls to the eval function. For Sphinx/SP1 cycles are reported at the end of proving. For Risc0 we use the user cycle count. For Jolt we use the reported trace length.

The three tables correspond to different sets of parameters used during proving described in Environment Variables below.

Fibonacci

Regular fibonacci (fib)

Input: 100000 (10^5)

Output: 2754320626097736315

Benchmark sources: Lurk, Sphinx, SP1, Risc0, Jolt

Default	Lurk	Sphinx	SP1	Risc0	Jolt
Setup	0.004 s	2.809 s	3.899 s	0.000 s	5.713 s
Prove	19.418 s	20.625 s	18.572 s	27.243 s	15.948 s
Verify	0.235 s	0.208 s	0.264 s	0.0268 s	0.378 s
Cycles	1,000,003	1,501,090	1,748,347	1,702,759	1,500,191
Memory	12.149 GiB	12.887 GiB	12.643 GiB	8.414 GiB	29.604 GiB

[A]	Lurk	Sphinx	SP1
Setup	0.004 s	3.033 s	4.313 s
Prove	15.766 s	10.788 s	13.052 s
Verify	0.234 s	0.297 s	0.365 s
Memory	12.105 GiB	9.872 GiB	10.188 GiB

[B]	Lurk	Sphinx	SP1
Setup	0.004 s	3.098 s	4.350 s
Prove	16.016 s	16.451 s	19.920 s
Verify	0.234 s	0.210 s	0.267 s
Memory	12.152 GiB	12.803 GiB	12.636 GiB

Fast fibonacci (fastfib)

Input: 18446744073709551614 (2^64 - 1)

Output: 16044305833753766745

Benchmark sources: Lurk, Sphinx, SP1, Risc0, Jolt

Default	Lurk	Sphinx	SP1	Risc0	Jolt
Setup	0.005 s	2.790 s	3.913 s	0.000 s	5.609 s
Prove	0.528 s	1.340 s	1.383 s	0.982 s	0.750 s
Verify	0.290 s	0.196 s	0.249 s	0.011 s	0.108 s
Cycles	4,821	7,387	11,245	9,379	6,549
Memory	0.211 GiB	2.301 GiB	3.278 GiB	0.708 GiB	0.632 GiB

[A]	Lurk	Sphinx	SP1
Setup	0.005 s	3.089 s	4.390 s
Prove	0.472 s	1.265 s	1.708 s
Verify	0.285 s	0.202 s	0.255 s
Memory	0.188 GiB	2.674 GiB	3.322 GiB

[B]	Lurk	Sphinx	SP1
Setup	0.005 s	3.129 s	4.323 s
Prove	0.472 s	1.276 s	1.452 s
Verify	0.285 s	0.199 s	0.252 s
Memory	0.192 GiB	2.668 GiB	3.327 GiB

Sum of vector (sum)

Input: 0..100000 (0..10^5)

Output: 4999950000

Benchmark sources: Lurk, Sphinx, SP1, Risc0, Jolt

Default	Lurk	Sphinx	SP1	Risc0	Jolt
Setup	1.938 s	2.882 s	3.989 s	0.000 s	0.959 s
Prove	18.612 s	221.433 s	275.728 s	596.713 s	178.446 s
Verify	0.237 s	0.581 s	2.295 s	0.567 s	13.118 s
Cycles	700,008	17,951,154	71,630,120	38,965,402	3,884,636
Memory	12.474 GiB	55.584 GiB	319.32 GiB	8.456 GiB	192.89 GiB

[A]	Lurk	Sphinx	SP1
Setup	2.055 s	3.075 s	4.337 s
Prove	15.881 s	82.700 s	222.915 s
Verify	0.252 s	1.764 s	8.052 s
Memory	12.457 GiB	104.494 GiB	94.949 GiB

[B]	Lurk	Sphinx	SP1
Setup	2.056 s	3.122 s	4.405 s
Prove	16.153 s	106.908 s	292.379 s
Verify	0.236 s	0.593 s	2.321 s
Memory	12.468 GiB	107.86 GiB	303.178 GiB

LCS (lcs/lcs2)

Input: (“When in the Course of human events, it becomes necessary for one people to dissolve the political bands which have connected them with another”, “There must be some kind of way outta here Said the joker to the thief. There’s too much confusion. I can’t get no relief.“)

Output: Any length 55 subsequence (e.g. “he e oe of a tt ee a e oe to the ti s ch connct et noe”, “here mst beome nay o e eoe to the ti s h connct et nor”)

For Rust-based zkVMs, there are two implementations of LCS (lcs and lcs2), indicated below separately. The Lurk numbers are repeated in both tables for comparison.

lcs

Benchmark sources: Lurk, Sphinx, SP1, Risc0, Jolt

Default	Lurk	Sphinx	SP1	Risc0	Jolt
Setup	0.005 s	2.790 s	3.954 s	0.000 s	7.866 s
Prove	7.943 s	20.168 s	9.553 s	27.168 s	15.741 s
Verify	0.238 s	0.207 s	0.264 s	0.026 s	0.454 s
Cycles	359,759	1,060,217	1,199,115	1,252,841	1,088,186
Memory	5.432 GiB	12.697 GiB	12.696 GiB	8.432 GiB	32.502 GiB

[A]	Lurk	Sphinx	SP1
Setup	0.005 s	3.148 s	4.306 s
Prove	7.306 s	9.483 s	12.328 s
Verify	0.239 s	0.293 s	0.376 s
Memory	5.404 GiB	8.024 GiB	8.788 GiB

[B]	Lurk	Sphinx	SP1
Setup	0.005 s	3.128 s	4.298 s
Prove	6.699 s	15.677 s	19.058 s
Verify	0.244 s	0.210 s	0.267 s
Memory	5.418 GiB	12.644 GiB	12.723 GiB

lcs2

Benchmark sources: Lurk, Sphinx, SP1, Risc0, Jolt

Default	Lurk	Sphinx	SP1	Risc0	Jolt
Setup	0.005 s	2.829 s	3.958 s	0.000 s	0.967 s
Prove	7.943 s	47.354 s	43.420 s	96.829 s	32.335 s
Verify	0.238 s	0.209 s	0.386 s	0.101 s	0.698 s
Cycles	359,759	3,622,427	5,033,647	4,773,346	3,566,186
Memory	5.432 GiB	26.966 GiB	25.210 GiB	8.434 GiB	65.846 GiB

[A]	Lurk	Sphinx	SP1
Setup	0.005 s	3.074 s	4.455 s
Prove	7.306 s	19.535 s	24.189 s
Verify	0.239 s	0.482 s	0.739 s
Memory	5.404 GiB	23.808 GiB	29.639 GiB

[B]	Lurk	Sphinx	SP1
Setup	0.005 s	3.079 s	4.324 s
Prove	6.699 s	36.767 s	46.019 s
Verify	0.244 s	0.212 s	0.390 s
Memory	5.418 GiB	26.901 GiB	25.394 GiB

Config

Environment Variables

• RUSTFLAGS="-C target-cpu=native -C opt-level=3"

The configurations below only apply to Sphinx/SP1 backends. They were chosen via benchmarking of our light clients (see docs for Aptos, Ethereum).

’Default’ parameters

Nothing is set or overridden, all defaults are used.

[A] parameters

For Lurk/Sphinx:

SHARD_SIZE=1048576 \
SHARD_CHUNKING_MULTIPLIER=1 \
SHARD_BATCH_SIZE=0 \
RECONSTRUCT_COMMITMENTS=false

For SP1, do not set SHARD_BATCH_SIZE=0 as it will not work.

[B] parameters

For Lurk/Sphinx:

SHARD_SIZE=4194304 \
SHARD_CHUNKING_MULTIPLIER=32 \
SHARD_BATCH_SIZE=0 \
RECONSTRUCT_COMMITMENTS=false

For SP1, do not set SHARD_BATCH_SIZE=0 as it will not work.

The parameter choices do two things:

Tweak SHARD_SIZE for more or fewer shards: Setting SHARD_SIZE lower increases parallelism (i.e. there are more shards, and they can be committed/proven in parallel) at the cost of more memory and increased verifier/recursion costs (i.e. the more shards, the more work the verifier needs to do). Same thing with the SHARD_CHUNKING_MULTIPLIER (though SHARD_SIZE is the main control knob. Here [A] has more shards (smaller shards) than [B] does.

Disable memory-saving codepaths for optimal performance. Setting RECONSTRUCT_COMMITMENTS=false (or any of the other variables) for example changes nothing except the prover just saves data in-memory instead of recalculating it, which is less work but uses more memory. Setting SHARD_BATCH_SIZE=0 disables checkpointing completely, so the proof needs to fit in working RAM since the prover will not flush intermediate artifacts to disk. These options are just “free” performance as long as the proof is not too large for the given prover (which is the case here). Here both options are using the same variables.

The latter is the same between both [A]/[B] layouts (i.e. they both disable the same checkpointing settings, making it faster at the cost of memory). The difference is in the sizes (and thus the amount) of shards, which changes how much parallelism is achievable in the proof. Generally, the more shards the more parallelism can help at a higher verifier cost. This is because committing to Merkle trees involves a lot of hashing which is very linear work (you can’t calculate a single hash using multiple threads, but you can calculate multiple hashes in multiple threads). Lowering shard size/increasing shard count means that more shards can be worked on in parallel, as a trade-off. This means even though [A] could have slightly lower prover costs, it does so at the expense of verifier costs (this is more pronounced in “recursive verifiers”, but is generally true).

Security Level

These benchmarks used standard FRI parameters targeting a conjectured security level of 116-bits for Lurk, Sphinx, and SP1 — and the default values for Risc0. The only outlier that does not use FRI is Jolt, which relies on the discrete logarithm problem for elliptic curves for its security arguments.

Specs

AWS r7iz.metal-32xl instance
Intel(R) Xeon(R) CPU @ 3.9GHz
128 vCPUs
1024GB DDR5 RAM

Full specs

NOTE: The r7iz.metal-32xl has the best CPU-only performance we’ve found in a commodity cloud machine for Sphinx and SP1. This is primarily due to the high vCPU and memory count, coupled with the Sapphire Rapids CPU architecture for recent AVX512 support.

Notes

The benchmark files can be found at https://github.com/argumentcomputer/zkvm-benchmarks

Update on Risc0 cycle counts (September 5, 2024): Previously we reported the Risc0 cycle count as the reported “total cycles” count, which actually includes, among other things, padding to the nearest power of 2. This was an oversight on our part since the padding should not have been considered. We have changed the values to the “user cycles” count, which does not include any padding or overhead from continuations, and should be a closer comparison with the Sphinx/SP1 RISC-V cycle counts.